数据挖掘作业一：线性回归、逻辑回归和支持向量机

发表于 | 分类于
字数统计： 22k | 阅读时长≈ 0:22

中山大学软件工程数据挖掘第一次作业

线性回归

某班主任为了了解本班同学的数学和其他科目考试成绩间关系，在某次阶段性测试中，他在全班学生中随机抽取1个容量为5的样本进行分析。该样本中5位同学的数学和其他科目成绩对应如下表：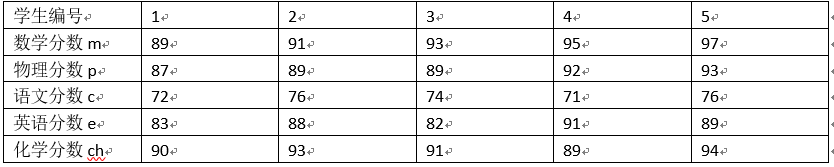
这里写图片描述
利用以上数据，建立m与其他变量的多元线性回归方程。

梯度下降法代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np

"""
梯度下降法
"""

# features scaling
def featuresNormalization(x):
    x_mean = np.mean(x, axis=0) # 列均值
    x_max = np.max(x, axis=0) # 列最大值
    x_min = np.min(x, axis=0) # 列最小值
    x_s = x_max - x_min
    x = (x - x_mean) / x_s
    return x, x_mean, x_s

# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, m, numIterations):
    x_T = np.transpose(x)
    for i in range(0, numIterations):
        hypothesis = np.dot(x, theta)
        loss = hypothesis - y
        # avg cost function J
        cost = np.sum(loss ** 2) / (2 * m)
        print("Iteration %d | Cost: %f" % (i, cost))
        # avg gradient per example
        gradient = np.dot(x_T, loss) / m
        # update theta
        theta = theta - alpha * gradient
        print("Iteration %d | Theta: %s" % (i, theta))
    return theta

# 数据
Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
              [89, 76, 88, 93],
              [89, 74, 82, 91],
              [92, 71, 91, 89],
              [93, 76, 89, 94]])
X, X_mean, X_s = featuresNormalization(X) # 特征值缩放
Y = np.array([89, 91, 93, 95, 97])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
n = np.alen(X[0])
alpha = 1
theta = np.zeros(n)

print(theta)
print(X)

# 6354可达到与sklearn相同的预测值
theta = gradientDescent(X, Y, theta, alpha, m, 6354)
print("Theta: ", theta)

x_predict = np.array([[88, 73, 87, 92]])
x_predict = (x_predict - X_mean) / X_s
m = np.alen(x_predict)
ones = np.ones(m)
x_predict = np.column_stack((ones, x_predict))
result = np.dot(x_predict, theta)
print("Predit result: %.4f" % result)

运行结果如下：
这里写图片描述

标准方程代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np

Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
              [89, 76, 88, 93],
              [89, 74, 82, 91],
              [92, 71, 91, 89],
              [93, 76, 89, 94]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
X_T = np.transpose(X)

# theta = (X'X)^(-1)X'Y
# theta = np.dot(np.dot(np.linalg.inv(np.dot(X_T, X)), X_T), Y)
temp1 = np.dot(X_T, X)
temp2 = np.linalg.inv(temp1)
temp3 = np.dot(temp2, X_T)
theta = np.dot(temp3, Y)
print("Theta: ", theta)

x_predit = [1, 88, 73, 87, 92]
print("Predit result: ", np.dot(x_predit, theta))

运行结果如下：
这里写图片描述

正则化的标准方程代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np

"""
正则化
"""

Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
              [89, 76, 88, 93],
              [89, 74, 82, 91],
              [92, 71, 91, 89],
              [93, 76, 89, 94]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
X_T = np.transpose(X)
lamda = 1
matrix = np.eye(np.alen(X))
matrix[0][0] = 0
# print(matrix)



# 无正则化
# theta = (X'X)^(-1)X'Y
# temp1 = np.dot(X_T, X)

# L2正则化
# theta = (X'X + lamda*matrix)^(-1)X'Y
temp1 = np.dot(X_T, X) + lamda * matrix

temp2 = np.linalg.inv(temp1)
temp3 = np.dot(temp2, X_T)
theta = np.dot(temp3, Y)
print("Theta: ", theta)

x_predit = [1, 88, 73, 87, 92]
print("Predit result: ", np.dot(x_predit, theta))

运行结果如下：
这里写图片描述

scikit-learn线性回归代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
from sklearn import linear_model

"""
scikit-learn
"""

Y = np.array([89, 91, 93, 95, 97])
X = np.array([[87, 72, 83, 90],
              [89, 76, 88, 93],
              [89, 74, 82, 91],
              [92, 71, 91, 89],
              [93, 76, 89, 94]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))

model = linear_model.LinearRegression()
model.fit(X, Y)
x_predict = np.array([[1, 88, 73, 87, 92]])
result = model.predict(x_predict)
print(model.intercept_)
print(model.coef_)
print("Predit result: ", result)

运行结果如下：
这里写图片描述

逻辑回归

研究人员对使用雌激素与子宫内膜癌发病间的关系进行了1:1配对的病例对照研究。病例与对照按年龄相近、婚姻状况相同、生活的社区相同进行了配对。收集了年龄、雌激素药使用、胆囊病史、高血压和非雌激素药使用的数据。变量定义及具体数据如下：
match：配比组
case：case=1病例；case=0对照（未发病）
est：est=1使用过雌激素；est=0未使用雌激素；
gall：gall=1有胆囊病史；gall=0无胆囊病史；
hyper：hyper=1有高血压；hyper=0无高血压；
nonest：nonest=1使用过非雌激素；nonest=0未使用过非雌激素；
表格略，表格的数据已在代码中体现。

简单逻辑回归代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import math
import numpy as np
from sklearn.cross_validation import train_test_split

def sigmoid(x):
    result = 1 / (1 + np.exp(-x))
    return result

# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, m, numIterations):
    x_T = np.transpose(x)
    y_T = np.transpose(y)
    for i in range(0, numIterations):
        hypothesis = sigmoid(np.dot(x, theta))
        loss = hypothesis - y
        # avg cost function J
        cost = 0 - (np.sum(np.dot(y_T, np.log(hypothesis)) + 
                np.dot(1 - y_T, 1 - np.log(hypothesis)))) / m
        print("Iteration %d | Cost: %f" % (i, cost))
        # avg gradient per example
        gradient = np.dot(x_T, loss) / m
        # update theta
        theta = theta - alpha * gradient
        print("Iteration %d | Theta: %s" % (i, theta))
    return theta

X = np.array([[1, 1, 0, 1], [0, 1, 0, 0],
              [1, 0, 1, 1], [0, 0, 0, 1],
              [1, 1, 0, 1], [1, 0, 1, 1],
              [1, 0, 0, 0], [1, 0, 1, 1],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 1, 0, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [1, 1, 1, 1], [0, 0, 1, 1],
              [1, 0, 0, 1], [1, 0, 0, 1],
              [0, 0, 0, 1], [0, 0, 0, 1],
              [1, 0, 1, 1], [1, 0, 1, 1],
              [0, 0, 0, 1], [0, 0, 1, 1],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [1, 0, 1, 1],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [0, 1, 0, 1], [0, 0, 1, 0],
              [1, 1, 0, 1], [1, 1, 0, 0],
              [1, 0, 0, 0], [1, 0, 1, 1]])

m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
Y = np.array([1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,
              1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0])
n = np.alen(X[0])

# 划分为训练集和测试集，测试集占1/5
X, X_test, Y, Y_test = train_test_split(X, Y, test_size=0.2)

theta = np.zeros(n)
alpha = 1
numIterations = 43000
theta = gradientDescent(X, Y, theta, alpha, m, numIterations)
print("Theta: ", theta)

predict = sigmoid(np.dot(X_test, theta))
# 将小于0.5的数置为0，将大于等于0.5的数置为1
predict = np.where(predict >= 0.5, predict, 0)
predict = np.where(predict < 0.5, predict, 1)

# 统计预测准确的数目
right = np.sum(predict == Y_test)
# 将预测值和真实值放在一块，便于观察
predict = np.hstack((predict.reshape(-1, 1), Y_test.reshape(-1, 1)))
print("Predict and Y_test: \n", predict)
# 计算在测试集上的准确率
print('测试集准确率：%f%%' % (right * 100.0 / predict.shape[0]))

运行结果如下：
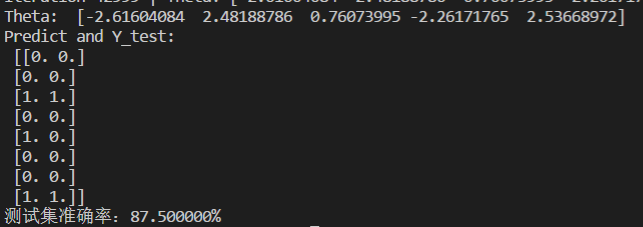
这里写图片描述

正则化代价函数的逻辑回归代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import math
import numpy as np
from sklearn.cross_validation import train_test_split

def sigmoid(x):
    result = 1 / (1 + np.exp(-x))
    return result

# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, lamda, m, numIterations):
    x_T = np.transpose(x)
    y_T = np.transpose(y)
    for i in range(0, numIterations):
        hypothesis = sigmoid(np.dot(x, theta))
        loss = hypothesis - y
        # avg cost function J
        cost = 0 - (np.sum(np.dot(y_T, np.log(hypothesis)) + np.dot(1 - y_T, 1 - np.log(hypothesis)))) / m 
        + lamda * np.sum(np.dot(theta.T, theta)) / (2 * m) 
        print("Iteration %d | Cost: %f" % (i, cost))
        # avg gradient per example
        gradient = np.dot(x_T, loss) / m
        # update theta
        theta = theta - alpha * (gradient + lamda * theta / m)
        print("Iteration %d | Theta: %s" % (i, theta))
    return theta

X = np.array([[1, 1, 0, 1], [0, 1, 0, 0],
              [1, 0, 1, 1], [0, 0, 0, 1],
              [1, 1, 0, 1], [1, 0, 1, 1],
              [1, 0, 0, 0], [1, 0, 1, 1],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 1, 0, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [1, 1, 1, 1], [0, 0, 1, 1],
              [1, 0, 0, 1], [1, 0, 0, 1],
              [0, 0, 0, 1], [0, 0, 0, 1],
              [1, 0, 1, 1], [1, 0, 1, 1],
              [0, 0, 0, 1], [0, 0, 1, 1],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [1, 0, 1, 1],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [0, 1, 0, 1], [0, 0, 1, 0],
              [1, 1, 0, 1], [1, 1, 0, 0],
              [1, 0, 0, 0], [1, 0, 1, 1]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
Y = np.array([1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,
              1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0])
n = np.alen(X[0])

# 划分为训练集和测试集，测试集占1/5
X, X_test, Y, Y_test = train_test_split(X, Y, test_size=0.2)

theta = np.zeros(n)
alpha = 1
lamda = 1
numIterations = 5000
theta = gradientDescent(X, Y, theta, alpha, lamda, m, numIterations)
print("Theta: ", theta)

predict = sigmoid(np.dot(X_test, theta))
# 将小于0.5的数置为0，将大于等于0.5的数置为1
predict = np.where(predict >= 0.5, predict, 0)
predict = np.where(predict < 0.5, predict, 1)

# 统计预测准确的数目
right = np.sum(predict == Y_test)
# 将预测值和真实值放在一块，便于观察
predict = np.hstack((predict.reshape(-1, 1), Y_test.reshape(-1, 1)))
print("Predict and Y_test: \n", predict)
# 计算在测试集上的准确率
print('测试集准确率：%f%%' % (right * 100.0 / predict.shape[0]))

运行结果如下：
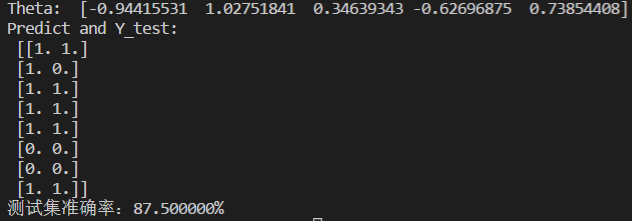
这里写图片描述

scikit-learn逻辑回归代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import train_test_split
import numpy as np

X = np.array([[1, 1, 0, 1], [0, 1, 0, 0],
              [1, 0, 1, 1], [0, 0, 0, 1],
              [1, 1, 0, 1], [1, 0, 1, 1],
              [1, 0, 0, 0], [1, 0, 1, 1],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 1, 0, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [1, 1, 1, 1], [0, 0, 1, 1],
              [1, 0, 0, 1], [1, 0, 0, 1],
              [0, 0, 0, 1], [0, 0, 0, 1],
              [1, 0, 1, 1], [1, 0, 1, 1],
              [0, 0, 0, 1], [0, 0, 1, 1],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [1, 0, 1, 1], [0, 0, 0, 0],
              [1, 0, 0, 1], [1, 0, 1, 1],
              [1, 0, 0, 1], [0, 0, 0, 0],
              [0, 1, 0, 1], [0, 0, 1, 0],
              [1, 1, 0, 1], [1, 1, 0, 0],
              [1, 0, 0, 0], [1, 0, 1, 1]])
m = np.alen(X)
ones = np.ones(m)
X = np.column_stack((ones, X))
Y = np.array([1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,
              1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0])
# 划分为训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)

# 逻辑回归
model = LogisticRegression()
model.fit(X_train, Y_train)
print("Theta: ", model.coef_)

# 预测
predict = model.predict(X_test)
right = sum(predict == Y_test)
# 将预测值和真实值放在一块，便于观察
predict = np.hstack((predict.reshape(-1, 1), Y_test.reshape(-1, 1)))
print("Predict and Y_test: \n", predict)
# 计算在测试集上的准确度
print('测试集准确率：%f%%' % (right*100.0 / predict.shape[0]))

运行结果如下：
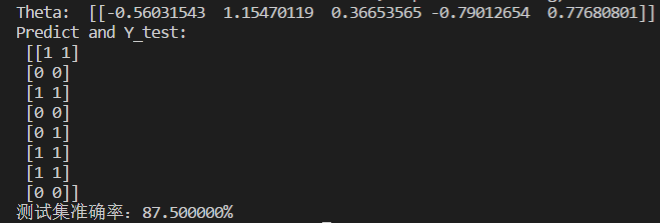
这里写图片描述

支持向量机

考虑以下的两类训练样本集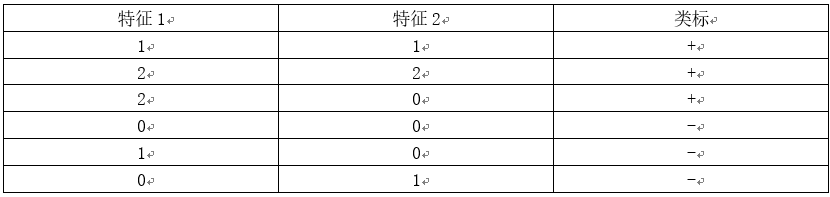
这里写图片描述

scikit-learn支持向量机代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import numpy as np
from matplotlib import pyplot as plt
from sklearn import svm 

    
# 作图
def plot_data(X, y):
    plt.figure(figsize=(10, 8))
    pos = np.where(y == 1) # 找到y==1的位置
    neg = np.where(y == 0) # 找到y==0的位置
    # np.ravel使多维矩阵降为一维
    p1, = plt.plot(np.ravel(X[pos, 0]), np.ravel(X[pos, 1]), 'rx', markersize=8)
    p2, = plt.plot(np.ravel(X[neg, 0]), np.ravel(X[neg, 1]), 'bo', markersize=8)
    plt.xlabel("X1")
    plt.ylabel("X2")
    plt.legend([p1, p2], ["y==+", "y==—"])
    return plt
    

def SVM(X, y, kernels='linear'):
    '''线性分类'''
    model = svm.SVC(C=1.0, kernel='linear').fit(X, y) # 指定核函数为线性核函数
    '''非线性分类'''
    # model = svm.SVC(gamma=100).fit(X, y) # gamma为核函数的系数，值越大拟合的越好

    plt = plot_data(X, y)
    
    # 画线性分类的决策边界
    if kernels == 'linear':
        theta12 = model.coef_ # theta1 and theta2
        theta0 = model.intercept_ # theta0
        print("Theta 1 and theta 2: ", theta12)
        print("Theta 0: ", theta0)
        print("k: ", -(theta12[0, 0] * 100) / (100 * theta12[0, 1]))
        print("b: ", float(-theta0 * 100 / (theta12[0, 1] * 100)))
        print("最优超平面（决策边界）的方程：y = %dx + %.1f" % (-(theta12[0, 0] * 100) / (100 * theta12[0, 1]), -theta0 / theta12[0, 1]))
        x1 = np.linspace(np.min(X[:, 0]), np.max(X[:, 0]), 100)
        x2 = -(theta12[0, 0] * x1 + theta0) / theta12[0, 1] # theta0 + theta1*x1 + theta2*x2 == 0
        plt.plot(x1, x2, 'green', linewidth=2.0)
        plt.show()
    # 画非线性分类的决策边界
    else:
        x_1 = np.transpose(np.linspace(np.min(X[:, 0]), np.max(X[:, 0]), 100).reshape(1, -1))
        x_2 = np.transpose(np.linspace(np.min(X[:, 1]), np.max(X[:, 1]), 100).reshape(1, -1))
        X1, X2 = np.meshgrid(x_1, x_2)
        vals = np.zeros(X1.shape)
        for i in range(X1.shape[1]):
            this_X = np.hstack((X1[:, i].reshape(-1, 1), X2[:, i].reshape(-1, 1)))
            vals[:, i] = model.predict(this_X)
        plt.contour(X1, X2, vals, [0, 1], color='green')
        plt.show()

X = np.array([[1, 1], [2, 2], [2, 0], [0, 0], [1, 0], [0, 1]])
y = np.array([1, 1, 1, 0, 0, 0])

plot_data(X, y)
SVM(X, y) # 线性分类画决策边界
# SVM(X, y, model, class_='notLinear') # 非线性分类画决策边界

运行结果如下：
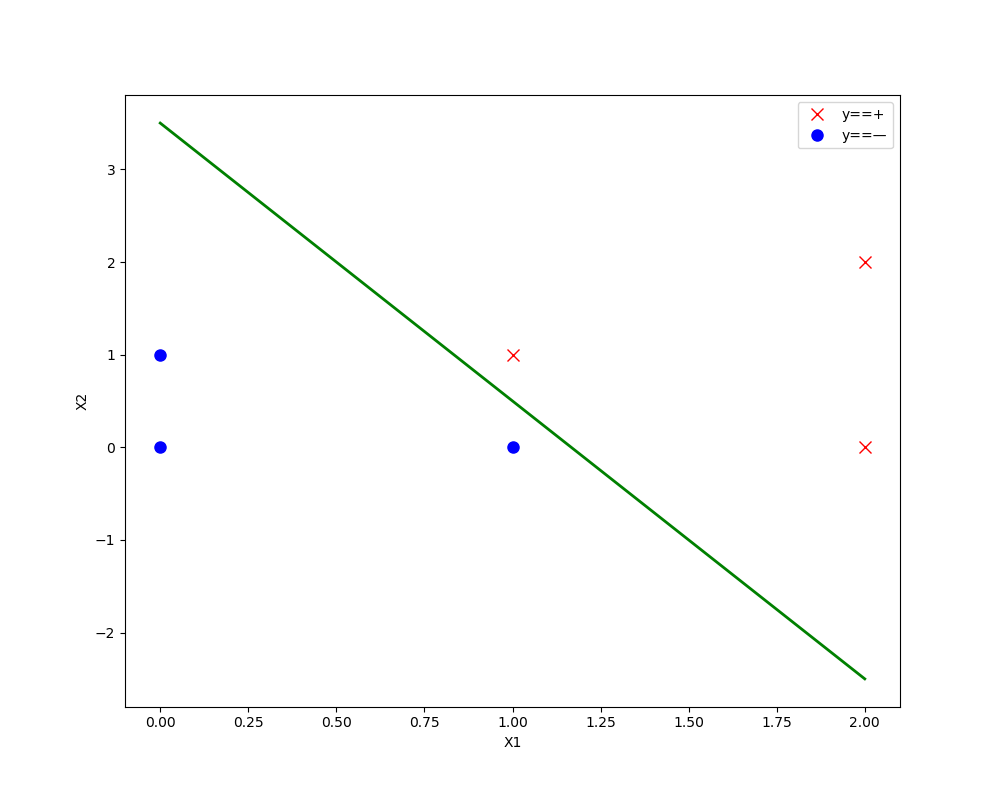
这里写图片描述
决策边界如下图：
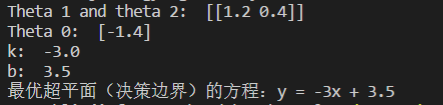
这里写图片描述

拉格朗日待定乘数求解代码如下：

SMO算法来自这个博客https://blog.csdn.net/willbkimps/article/details/54697698

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import numpy as np
from numpy import *
from time import sleep  
from matplotlib import pyplot as plt
  
#加载文本文件中的数据，返回数据矩阵和类标签  
def loadDataSet(fileName):  
    dataMat = []; labelMat = []  
    fr = open(fileName)  
    for line in fr.readlines():  
        lineArr = line.strip().split('\t')  
        dataMat.append([float(lineArr[0]), float(lineArr[1])])  
        labelMat.append(float(lineArr[2]))  
    return dataMat,labelMat  
  
#随机选择不等于i的值。i是第一个α的下表，m是α的数量  
def selectJrand(i,m):  
    j=i #we want to select any J not equal to i  
    while (j==i):  
        j = int(random.uniform(0,m))  
    return j  
  
#调整大于H或小于L的α值  
def clipAlpha(aj,H,L):  
    if aj > H:  
        aj = H  
    if L > aj:  
        aj = L  
    return aj

#dataMatIn, classLabels, C, toler, maxIter分别为数据集、类标签、常数C、容错率和最大迭代次数  
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):  
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()  
    b = 0; m,n = shape(dataMatrix)  
    alphas = mat(zeros((m,1)))  
    iter = 0  
    while (iter < maxIter):  
        alphaPairsChanged = 0  
        for i in range(m):  
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b  
            Ei = fXi - float(labelMat[i])  
               #if checks if an example violates KKT conditions  
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):  
                j = selectJrand(i,m)  
                fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b  
                Ej = fXj - float(labelMat[j])  
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();  
                #将α的值调整到区间[0,C]  
                if (labelMat[i] != labelMat[j]):  
                    L = max(0, alphas[j] - alphas[i])  
                    H = min(C, C + alphas[j] - alphas[i])  
                else:  
                    L = max(0, alphas[j] + alphas[i] - C)  
                    H = min(C, alphas[j] + alphas[i])  
                if L==H: print ("L==H"); continue  
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T  
                if eta >= 0: print ("eta>=0"); continue  
                #对αi和αj进行修改，αi的修改量和αj相同，但方向相反  
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta  
                alphas[j] = clipAlpha(alphas[j],H,L)  
                if (abs(alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); continue  
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j  
                                                                        #the update is in the oppostie direction  
                #b的更新  
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T  
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T  
                if (0 < alphas[i]) and (C > alphas[i]): b = b1  
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2  
                else: b = (b1 + b2)/2.0  
                alphaPairsChanged += 1  
                print ("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))  
        if (alphaPairsChanged == 0): iter += 1  
        else: iter = 0  
        print ("iteration number: %d" % iter  )
    return b,alphas

dataMat,labelMat = loadDataSet('D:\linjiafengyang\Code\Python\SupportVectorMachine\smo.txt')
C = 1
toler = 0.001
maxIter = 200
b,alphas = smoSimple(dataMat, labelMat, C, toler, maxIter)
print(alphas)
print(b)

alphas = np.array(alphas)
labelMat = np.array(labelMat)

theta12 = (alphas.T*labelMat).dot(dataMat)
print(theta12)
theta0 = theta12[0,0]
theta1 = theta12[0,1]
k = -theta0 / theta1
b = -b / theta1
print("k: %.1f" % k)
print("b: %.1f" % b)
print("最优超平面（决策边界）的方程：y = %.1fx + %.1f" % (k, b))

运行结果如下：
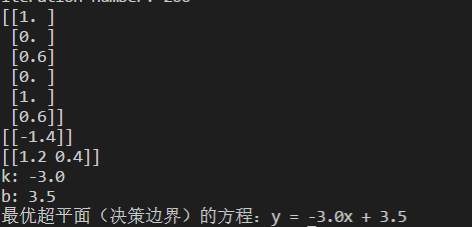
这里写图片描述

matlab版本的SMO算法：参考这位真大佬https://blog.csdn.net/on2way/article/details/47730367
虽然代码有点小纰漏，我已经在我自己的代码改过来了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
%%
% * svm 简单算法设计
%
%% 加载数据
% * 最终data格式：m*n，m样本数，n维度
% * label:m*1  标签必须为-1与1这两类
clc
clear
close all
data = load('mydata.mat');
data = data.A;
train_data = data(1:end-1,:)';
label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
% 系数
b = 0;
% 松弛变量影响因子
C = 1;
iter = 0;
max_iter = 40;
%%
while iter < max_iter
    alpha_change = 0;
    for i = 1:num_data
        %输出目标值
        pre_Li = (alphas.*label)'*(data*data(i,:)') + b;
        %样本i误差
        Ei = pre_Li - label(i);
        % 满足KKT条件
        if (label(i)*Ei<-0.001 && alphas(i)<C)||(label(i)*Ei>0.001 && alphas(i)>0)
           % 选择一个和 i 不相同的待改变的alpha(2)--alpha(j)
            j = randi(num_data,1);  
            if j == i
                temp = 1;
                while temp
                    j = randi(num_data,1);
                    if j ~= i
                        temp = 0;
                    end
                end
            end
            % 样本j的输出值
            pre_Lj = (alphas.*label)'*(data*data(j,:)') + b;
            %样本j误差
            Ej = pre_Lj - label(j);
            %更新上下限
            if label(i) ~= label(j) %类标签相同
                L = max(0,alphas(j) - alphas(i));
                H = min(C,C + alphas(j) - alphas(i));
            else
                L = max(0,alphas(j) + alphas(i) -C);
                H = min(C,alphas(j) + alphas(i));
            end
            if L==H  %上下限一样结束本次循环
                continue;end
            %计算eta
            eta = 2*data(i,:)*data(j,:)'- data(i,:)*data(i,:)' - ...
                data(j,:)*data(j,:)';
            %保存旧值
            alphasI_old = alphas(i);
            alphasJ_old = alphas(j);
            %更新alpha(2)，也就是alpha(j)
            alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
            %限制范围
            if alphas(j) > H
                alphas(j) = H;
            elseif alphas(j) < L
                    alphas(j) = L;
            end
            %如果alpha(j)没怎么改变，结束本次循环
            if abs(alphas(j) - alphasJ_old)<1e-4
                continue;end
            %更新alpha(1)，也就是alpha(i)
            alphas(i) = alphas(i) + label(i)*label(j)*(alphasJ_old-alphas(j));
            %更新系数b
            b1 = b - Ei - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(i,:)'-...
                label(j)*(alphas(j)-alphasJ_old)*data(i,:)*data(j,:)';
            b2 = b - Ej - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(j,:)'-...
                label(j)*(alphas(j)-alphasJ_old)*data(j,:)*data(j,:)';
            %b的几种选择机制
            if alphas(i)>0 && alphas(i)<C
                b = b1;
            elseif alphas(j)>0 && alphas(j)<C
                b = b2;
            else
                b = (b1+b2)/2;
            end
            %确定更新了，记录一次
            alpha_change = alpha_change + 1;
        end
    end
    % 没有实行alpha交换，迭代加1
    if alpha_change == 0
        iter = iter + 1;
    %实行了交换，迭代清0
    else
        iter = 0;
    end
    disp(['iter ================== ',num2str(iter)]);
end
%% 计算权值W
W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*(data*data') + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))';
plot(data1(1,:),data1(2,:),'bo');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))';
plot(data2(1,:),data2(2,:),'r+');
hold on
%dataw = (data(index_sup,:))';
%plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
% 画出分界面，以及b上下正负1的分界面
hold on
k = -W(1)/W(2);
b = - b / W(2);
x = 0:0.1:2.5;
y = k*x + b;
plot(x,y,'green',x,y-1,'r--',x,y+1,'r--');
title(['松弛变量范围C = ',num2str(C)]);

运行结果如下：
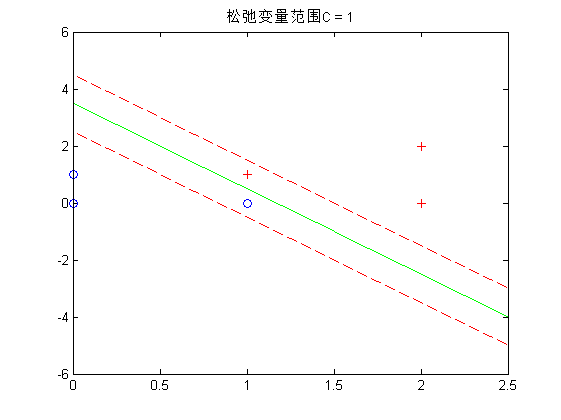
这里写图片描述
决策边界（绿色线）以及支持向量（红色线）如下：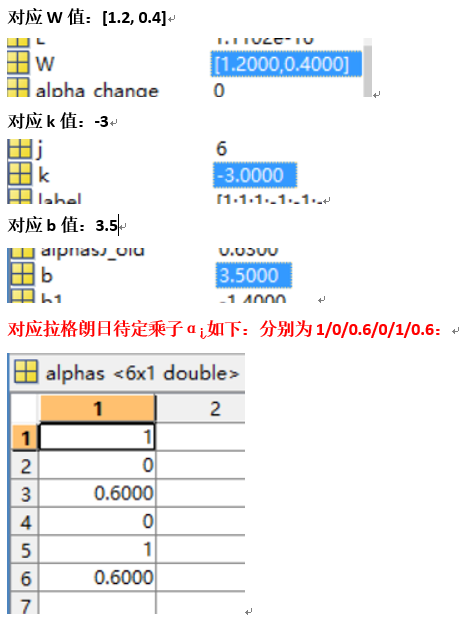
这里写图片描述

作业思考

  1. 线性回归与逻辑回归的区别：
    线性回归主要用来解决连续值预测的问题，逻辑回归用来解决分类的问题，输出的属于某个类别的概率。
  2. 逻辑回归与支持向量机的区别：
    两种方法都是常见的分类算法，两者的根本目的都是一样的。
    目标函数：逻辑回归采用的是logistical loss，svm采用的是hinge loss。这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。
    训练样本点：SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。
    简单性：逻辑回归相对来说模型更简单，容易实现，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些。但是SVM的理论基础更加牢固，有一套结构化风险最小化的理论基础，虽然一般使用的人不太会去关注。还有很重要的一点，SVM转化为对偶问题后，分类只需要计算与少数几个支持向量的距离，这个在进行复杂核函数计算时优势很明显，能够大大简化模型和计算量。
------本文结束感谢阅读------